Analysis of the Wave Energy Reduction of Rubble Mound Breakwaters
Emerged Breakwater - Wave Height
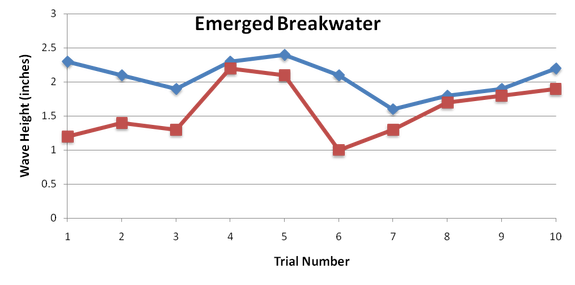
This graph is a simple plot of the observed wave height before and after the breakwater model for the emerged testing. There were 10 trials ran (x-axis) and a wave height was collected for each, which is represented on the y-axis in inches. The blue line represents the wave height reading before the water crossed the breakwater model. The red line represents the wave height after the wave crossed the breakwater model.
There is slight variation in this graph (specifically Trial 4, 8, and 9) because of human error and initial wave generation techniques.
There is slight variation in this graph (specifically Trial 4, 8, and 9) because of human error and initial wave generation techniques.
Submerged Breakwater - Wave Height
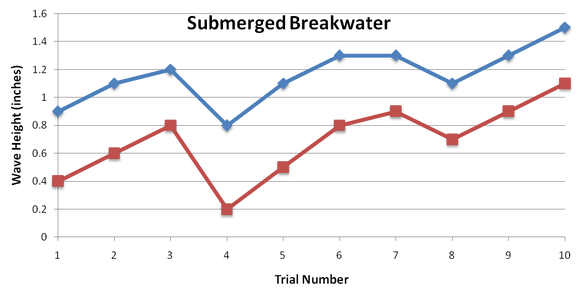
This graph is a simple plot of the observed wave height before and after the breakwater model for the submerged testing. There were 10 trials ran (x-axis) and a wave height was collected for each, which is represented on the y-axis in inches. The blue line represents the wave height reading before the water crossed the breakwater model. The red line represents the wave height after the wave crossed the breakwater model. The wave height difference between the before and after breakwater measurements stay very consistent over the 10 trial runs. This is due to the user becoming more comfortable generating the waves and doing so more consistently.
Emerged Breakwater - Wave Energy
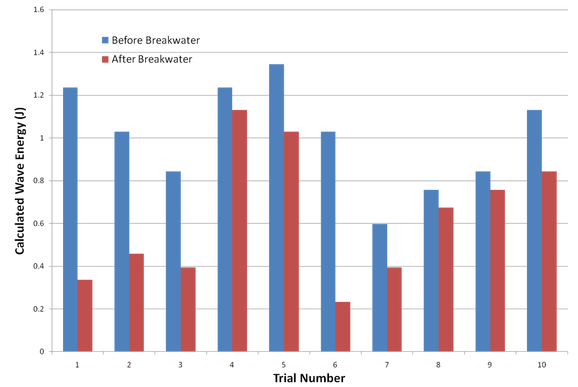
The graph to the left is one that displays the calculated wave energy for each trial of the emerged breakwater testing, while also comparing the energy (in Joules) before the breakwater model (blue) and after the breakwater. Before the wave energy was calculated the wave length had to be calculated from the average wave period which was collected throughout the trials. The average wave period of the between the emerged trials was 0.8 seconds. Using the set of equations: L=1.56(T^2), L1=L(0)*sqrt(tanh((2*pi)/L(0))*SWL)), L2=L(0)*tanh((2*pi)/L(1))*SWL), and finally L=(L1 + L2)/2. The calculated emerged wave length was 11.83 inches.
Wave energy was then calculated because we thought that this would be the best indicator for how much erosion would be done to the shore and coastline. This was done using the equation: E=[(L*1000*9.81)*(H^2)]/8. This is where the calculated values on the graph to the right are derived from.
Wave energy was then calculated because we thought that this would be the best indicator for how much erosion would be done to the shore and coastline. This was done using the equation: E=[(L*1000*9.81)*(H^2)]/8. This is where the calculated values on the graph to the right are derived from.
Submerged Breakwater - Wave Energy
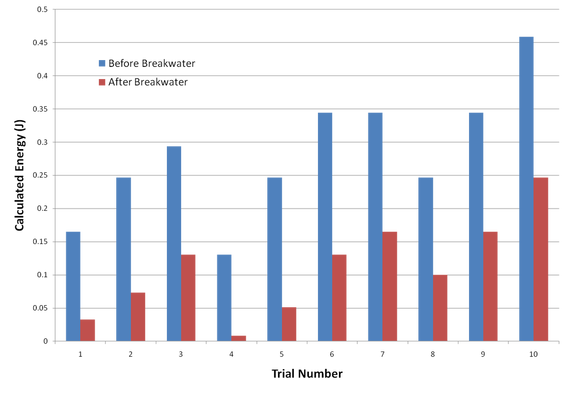
The graph to the left is one that displays the calculated wave energy for each trial of the submerged breakwater testing, while also comparing the energy (in Joules) before the breakwater model (blue) and after the breakwater. The same calculations as above were applied to the submerged data. The average observed wave period was 0.75 seconds, and the calculated emerged wave length was 10.33 inches.
The fluctuations in wave energy are directly tied to the wave height. If you compare this graph to the submerged wave height graph you can see the same pattern in wave height and wave energy fluctuation.
The fluctuations in wave energy are directly tied to the wave height. If you compare this graph to the submerged wave height graph you can see the same pattern in wave height and wave energy fluctuation.
**Average Wave Energy Reduction
The final analysis in our project was to compare the average wave energy reduction before and after the breakwater model comparing the emerged and submerged data. The calculated results were an Emerged Breakwater Reduction of 37.12% and a Submerged Breakwater Reduction of 65.11%. These results were not originally what we were expecting, but they indicate that submerged breakwaters adequately perform the same function as emerged breakwaters with a higher aesthetic appeal. We think that this percentage could change though if we made future improvements and a few changes to the modeling set up (discussed in ‘Model and Testing’).
